What better day to post my first mathematical blog post ever than \(\pi\)-day!
A classic XKCD comic is the one introducing the concept of ‘nerd sniping’:
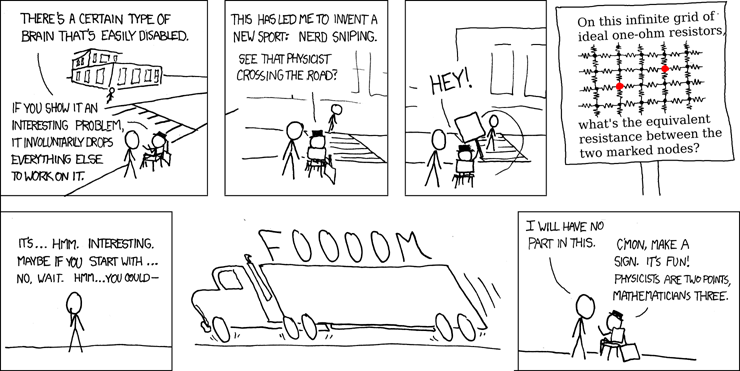
The challenge included in the comic is: On an infinite grid of $1\Omega$ resistors, what is the equivalent resistance between coordinates $(0, 0)$ and $(2, 1)$. The exact solution is $\frac{4}{\pi} - \frac{1}{2} \approx 0.773$ and a very extensive analytical derivation of that result can be found here. In this post we approach the challenge posed in a numerical (and therefore approximate) fashion, because who needs complex analytical derivations, when you can have a simple numerical solution, right?
Finite grid size
Let’s start on a finite grid size. We put a border of thickness $N$ around the minimal network containing points $(0, 0)$ and $(2, 1)$. This means we have a grid of $(2N + 2) \times (2N + 1)$ squares. This grid will have $(2N + 3) \times (2N + 2)$ nodes. We start with $N = 2$ now. Later we will investigate the convergence behavior for $N \to \infty$. We’ll need Ohm’s law and the Kirchoff laws. As
\[R = \frac{V}{I}\]we can either
- impose a voltage difference and compute the current from point $A = (0, 0)$ to point $B = (2, 1)$, or
- impose source current and sink current (of $1A$) equally at points $A$ and $B$ and compute the resulting voltage difference We have implemented the latter.
We’ll also need Ohm’s law on a per edge basis: Every edge has a $1\Omega$ resistor so:
\[\forall \text{ nodes } a, b \in n(a): V_b - V_a = I_{a \to b}\]The first law of Kirchoff conveys conservation of electrical charge: At any node in the electrical network, the sum of incoming currents equals the sum of outgoing currents. If we use positive and negative signs for currents consistently through the network, this becomes very simple:
\[\forall \text{ nodes } a: \sum_{b \in n(a)} I_{a \to b} = 0\]Where $n(a)$ is the set of neighboring nodes to node $a$. As stated above, the only points for which this is a bit nuanced are points $A$ and $B$, where we have imposed an additional source/sink current. Kirchoff’s second law will be satisfied naturally.
The above equations are all linear in the variables $I_{a \to b}$ and $V_a$. We’ll only need linear algebra to get to our solution.
Let’s setup the linear system to be solved. With $N=2$, we’ll have $7 \times 6 = 42$ nodes in the graph, $ 6 \times 6 = 36$ horizontal edges/resistors and $7 \times 5$ vertical ones. This means we’ll have $42$ voltage variables $V$, $36$ horizontal current variables $I_x$ and $35$ vertical current variables $I_y$. We have $113$ variables in total.
%matplotlib notebook
import numpy as np
import matplotlib.pyplot as plt
N = 2
pA = (N, N)
pB = (N + 2, N + 1)
nx = 2*N + 3
ny = 2*N + 2
Vs = np.empty((nx, ny))
Ix = np.empty((nx-1, ny))
Iy = np.empty((nx, ny-1))
print(Vs.size, Ix.size, Iy.size)
42 36 35
We introduce some helper variables to help out with the sizes. Numpy’s ravel and unravel functions we’ll be able to put to good use as well for conversion between 2D indices on a grid and 1D indices in the flattened variable space of the linear system. For this to work, we do put the lower left corner of the finite grid at the origin. This means we’ll need to shift the points $A$ and $B$ as well.
nV = 0
nIx = Vs.size
nIy = Vs.size + Ix.size
n_v = Vs.size + Ix.size + Iy.size
np.ravel_multi_index([1, 2], [2, 3])
5
np.unravel_index(5, [2, 3])
(1, 2)
We start with an empty list of equations and will append until it is complete. We use notation $Ax = b$ for the linear system.
A = []
b = []
We first loop over all currents running in the $x$ direction and construct the equation $V_b - V_a = I_{a \to b}$
for i in range(Ix.shape[0]):
for j in range(Ix.shape[1]):
a = np.zeros(n_v)
#V_A - V_B = I
i_VA = np.ravel_multi_index([i, j], Vs.shape)
i_VB = np.ravel_multi_index([i+1, j], Vs.shape)
i_I = np.ravel_multi_index([i, j], Ix.shape)
a[nV + i_VA] = 1
a[nV + i_VB] = -1
a[nIx + i_I] = -1
A.append(a)
b.append(0.)
plt.figure(figsize=(6, 2))
plt.spy(np.array(A))
In the spy plot, it is clear that every included equation until now involves three variables: 2 voltages (ordered first) and 1 current.
# Voltages across resistors
## Loop over y currents
for i in range(Iy.shape[0]):
for j in range(Iy.shape[1]):
a = np.zeros(n_v)
#V_A - V_B = I
i_VA = np.ravel_multi_index([i, j], Vs.shape)
i_VB = np.ravel_multi_index([i, j+1], Vs.shape)
i_I = np.ravel_multi_index([i, j], Iy.shape)
a[nV + i_VA] = 1
a[nV + i_VB] = -1
a[nIy + i_I] = -1
A.append(a)
b.append(0.)
plt.figure(figsize=(6, 4))
plt.spy(np.array(A))
The linear system has doubled in size. The new equations also have 3 nonzeros per row, but the voltages are now adjacent, due to the order in the 2D numpy arrays. The currents in $y$ are in the columns most to the right.
Next up are the current conservations per knot. Edges of the grid are handled with try/except and note the RHS is set to nonzero only for points $A$ and $B$
for i in range(Vs.shape[0]):
for j in range(Vs.shape[1]):
a = np.zeros(n_v)
# sum(I) = 0
## X
### Lower
try:
k = np.ravel_multi_index([i-1, j], Ix.shape)
a[nIx + k] = 1
except:
pass
### Upper
try:
k = np.ravel_multi_index([i, j], Ix.shape)
a[nIx + k] = -1
except:
pass
## Y
### Lower
try:
k = np.ravel_multi_index([i, j-1], Iy.shape)
a[nIy + k] = 1
except:
pass
### Upper
try:
k = np.ravel_multi_index([i, j], Iy.shape)
a[nIy + k] = -1
except:
pass
A.append(a)
if i == pA[0] and j == pA[1]:
b.append(-1.)
elif i == pB[0] and j == pB[1]:
b.append(1.)
else:
b.append(0.)
A = np.array(A)
b = np.array(b)
plt.figure(figsize=(6, 6))
plt.spy(A)
The new equations generally have 4 nonzeros per row, corresponding to 4 indicing edges for the internal nodes.
A.shape
(113, 113)
Though this matrix is square, it is singular. Physically this can be understood as we have not specified any absolute voltage yet, but have only worked with differences. The nullspace is expected to be 1D, and will be a global offset on voltages.
plt.figure()
plt.semilogy(np.linalg.svd(A)[1], 'o')
There are plenty of ways of dealing with this:
pinvwill work just fine on small systems due to its property of returning the solution closest to the origin inside the non-zero dimensional solution space.- We can add an voltage normalizing equations like $V_{(0, 0)} = 0$. This would make a non-rectangular system, such that a direct linear solver would have to be or QR type.
- We can replace one of the dependant equations we the above normalizing equation, retaining squareness.
plt.figure(figsize=(6, 2))
plt.plot(b, '.-')
sol = np.linalg.pinv(A) @ b
Vs_sol = sol[:nIx]
Ix_sol = sol[nIx:nIy]
Iy_sol = sol[nIy:]
Vs_sol.shape = Vs.shape
Ix_sol.shape = Ix.shape
Iy_sol.shape = Iy.shape
R_total = (Vs_sol[pA] - Vs_sol[pB])/1. #Current is 1
print(R_total)
0.8461880505301251
We get an estimate of $R = 0.84 \Omega$ on this small grid. Note that we have written our own basic nodal analysis method from scratch, as implemented in circuit simulators like SPICE.
Let’s scale up to get a more accurate value!
Scaling up!
We now repeat for larger grid sizes. We now use a sparse linear solver to solve. We also setup the linear system as a sparse one from the go. Scipy recommends using the lil_matrix format for that, rather than the csr_matrix.
import scipy.sparse.linalg
Ns = [2, 3, 4, 5, 6, 10, 15, 20, 30, 50, 100]
R_totals = []
for N in Ns:
pA = (N, N)
pB = (pA[0]+2, pA[1]+1)
nx = 2*N + 3
ny = 2*N + 2
Vs = np.empty((nx, ny))
Ix = np.empty((nx-1, ny))
Iy = np.empty((nx, ny-1))
nV = 0
nIx = Vs.size
nIy = Vs.size + Ix.size
n_v = Vs.size + Ix.size + Iy.size
A = scipy.sparse.lil_matrix((n_v, n_v)) #Recommended for matrix creation
b = np.zeros(n_v)
# Normalize lower left voltage
row = 0
A[row, 0] = 1
b[row] = 0
row += 1
# Voltages across resistors
## Loop over x currents
for i in range(Ix.shape[0]):
for j in range(Ix.shape[1]):
if i == 0 and j == 0:
continue
#V_A - V_B = I
i_VA = np.ravel_multi_index([i, j], Vs.shape)
i_VB = np.ravel_multi_index([i+1, j], Vs.shape)
i_I = np.ravel_multi_index([i, j], Ix.shape)
A[row, nV + i_VA] = 1
A[row, nV + i_VB] = -1
A[row, nIx + i_I] = -1
b[row] = 0.
row += 1
# Voltages across resistors
## Loop over x currents
for i in range(Iy.shape[0]):
for j in range(Iy.shape[1]):
#V_A - V_B = I
i_VA = np.ravel_multi_index([i, j], Vs.shape)
i_VB = np.ravel_multi_index([i, j+1], Vs.shape)
i_I = np.ravel_multi_index([i, j], Iy.shape)
A[row, nV + i_VA] = 1
A[row, nV + i_VB] = -1
A[row, nIy + i_I] = -1
b[row] = 0.
row += 1
# Current conservation at knots
for i in range(Vs.shape[0]):
for j in range(Vs.shape[1]):
# sum(I) = 0
## X
### Lower
try:
k = np.ravel_multi_index([i-1, j], Ix.shape)
A[row, nIx + k] = 1
except:
pass
### Upper
try:
k = np.ravel_multi_index([i, j], Ix.shape)
A[row, nIx + k] = -1
except:
pass
## Y
### Lower
try:
k = np.ravel_multi_index([i, j-1], Iy.shape)
A[row, nIy + k] = 1
except:
pass
### Upper
try:
k = np.ravel_multi_index([i, j], Iy.shape)
A[row, nIy + k] = -1
except:
pass
if i == pA[0] and j == pA[1]:
b[row] = -1.
elif i == pB[0] and j == pB[1]:
b[row] = 1.
else:
b[row] = 0.
row += 1
A = scipy.sparse.csr_matrix(A)
sol = scipy.sparse.linalg.spsolve(A, b)
Vs_sol = sol[:nIx]
Ix_sol = sol[nIx:nIy]
Iy_sol = sol[nIy:]
Vs_sol.shape = Vs.shape
Ix_sol.shape = Ix.shape
Iy_sol.shape = Iy.shape
R_total = (Vs_sol[pA] - Vs_sol[pB])/1. #Current is 1
print(N, R_total, A.shape)
R_totals.append(R_total)
2 0.8404735764243272 (113, 113)
3 0.8130316366934071 (199, 199)
4 0.7991933109798373 (309, 309)
5 0.7903559050121077 (443, 443)
6 0.7867792904859598 (601, 601)
10 0.7788855583785843 (1473, 1473)
15 0.7758654332069974 (3103, 3103)
20 0.7747765747933268 (5333, 5333)
30 0.7739448797740112 (11593, 11593)
50 0.7735010188754745 (31313, 31313)
100 0.7733064009494379 (122613, 122613)
4/np.pi - 1/2
0.7732395447351628
We get 3 correct digits when we solve it as a problem with 11k variables. The convergence plots below shows a monotonically decreasing behavior. This can be understood physically: As there are more and more pathways for the current to take, the overall resistance becomes lower.
plt.figure()
plt.plot(Ns, R_totals, '-o')
plt.plot(Ns, (4/np.pi - 1/2)*np.ones_like(Ns), '--', label='Exact value')
plt.xlabel('Grid radius')
plt.ylabel('Resistance [Ohm]')
Text(0, 0.5, 'Resistance [Ohm]')
plt.figure()
x = np.arange(1, 1000)
plt.loglog(Ns, np.array(R_totals) - (4/np.pi - 1/2), '-o')
plt.loglog(x, 0.1*1/x, '--', label='1/x')
plt.loglog(x, 1/x**2, '--', label='1/x^2')
plt.legend()
The convergence behavior seems to be quadratic with grid radius $N$.
Notes on computation speed
Note that the linear solve is still below 1 second on my laptop as we are dealing with a sparse problem with a 2D structure. At this problem size, the current setup, even though using sparse matrices, is still dominating the solve. Explicit Python loops are slow…
A.shape
(122613, 122613)
%%timeit
sol = scipy.sparse.linalg.spsolve(A, b)
675 ms ± 41.4 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
The linear system has rows consisting of $1$ and $-1$ entries, similar to finite differences of a first order derivative in partial differential equations on a grid. The normal form $A^TAx = A^Tb$ of these linear equations will resemble 2D Poisson equations very much. This makes the system very suited for solving with multigrid methods which have linear complexity in the number of variables. I used MG methods in my Masters thesis in Mathematical Engineering and am still fond of them to this day due to their incredible performance. Perhaps I’ll make a blog post about that one day as well…
Closing remarks
As we are publishing this on $\pi$-day, let’s not forget that we can use this method to estimate $\pi$. Note that we achieve this by solving a sparse matrix containing only zeros, ones and minus ones, and a right-hand side which is completely zero except for one one, and one minus one.
R = 0.7733064009494379
pi_approx = 4/(R + 1/2)
print(np.pi, pi_approx, np.pi - pi_approx)
3.141592653589793 3.1414277011545764 0.00016495243521674752
We get 4 correct significant digits from a ~200x200 grid.
I expect this approach to correspond to one of the known $\pi$ infinite series. Kudos to anyone who can tell me which one!
Related posts
None yet
Want to leave a comment?
Very interested in your comments but still figuring out the most suited approach to this. For now, feel free to send me an email or reply to this tweet.